Overview

ステッピングモーターを用いた二輪移動システムの滑らかな駆動の為に、三次曲線を用いたＳ字加減速の方程式を求めました。
その方程式と実際に動かした時の挙動を紹介します。

直進
直進は、加速区間、定速区間、減速区間の３つの区間で構成されます。現在の速度から最高速度に達するまで加速する加速区間と、最高速度を維持したまま走行する定速区間、そして、最高速度から元の速度まで減速する減速区間です。
方向転換(片回転方式)
停止状態から外輪のみを回転させて方向転換を行う方式です。外輪は加速・定速・減速を行います。片輪のみの駆動なので消費電力が抑えられるかもしれません。方向転換には比較的広い空間が必要です。
方向転換(逆回転方式)
停止状態から両輪を逆回転させて方向転換を行う方式です。両輪共に加速・定速・減速を行います。狭い空間でも方向転換が可能です。
進路変更
定速で走行中に外輪の速度を上げて進路変更を行います。外輪は加速・定速・減速を行います。内輪は一定速度を維持します。

まず、方程式で用いる変数の定義します。

変数名	意味	単位	値
$v_L$	元の速度	steps/sec	0～
$v_H$	最高速度	steps/sec	0～
acceleration	加速率	$steps/sec^2$	0～
deacceleration	減速率	$steps/sec^2$	0～
$t_a$	加速区間の時間	sec
$t_d$	減速区間の時間	sec
$S_a$	加速区間の移動距離	steps
$S_d$	減速区間の移動距離	steps
$spm$ ※1	1mmあたりのステップ数	steps/mm	1.1169
$\theta$	進行方向の角度	degree	-360～+360
$Rc$	旋回半径	mm	0～
$Lwh$	車輪間の距離	mm	196

※1 $$ spm = \frac{360}{モーターの1ステップあたりの角度 * 車輪の直径 * \pi} = \frac{360}{1.8 * 57 * \pi} $$

直進

加速区間

直進における加速区間における時間ごとの加速度・速度・距離と、加速区間の時間を求める方程式を求め、最後に例をグラフに描画して確認します。

加速の式

$$ t=0, t={t_a} の時に加速度がゼロになる二次方程式を立てる。$$ $$ a(t) = p * t * (t - {t_a})) $$ $$ a(\frac{t_a}{2}) = acceleration であるので、pについて解くと$$ $$ p=-\frac{4*acceleration}{t_a^2} $$ $$ pを上式に代入すると加速の式が得られる。 $$ $$ a(t) = \frac{4 * acceleration * t * (t_a - t)}{t_a^2} $$

速度の式

$$ 時間ごとの速度は次の式で表される。 $$ $$ v(t) = \int a(t) dt + v_L = v_L + \frac{2 * acceleration * t^2 * (3 * t_a - 2 * t)}{3 * t_a^2} $$

距離の式

$$ 時間ごとの距離は次の式で表される。 $$ $$ S_a(t) = \int v(t) dt = v_L * t + \frac{acceleration * t^3 * (2 * t_a - t)}{3 * t_a^2} $$

加速区間の時間

$$ v(t_a)={v_H}であるので、{t_a}について解くと $$ $$ {t_a} = \frac{3*(v_H - v_L)}{2 * acceleration} $$

加速区間の方程式をグラフで確認します。
条件を $v_L=100, v_H=400, acceleration=100$ として計算すると $$ t_a=4.5 $$ $$ S_a(t_a)=1125 $$ となります。

Destop View

減速区間

直進における減速区間も加速区間と同様の方法で方程式を立てます。

減速の式

$$ a(t) = - \frac{4 * deacceleration * t * (t_d - t)}{t_d^2} $$

速度の式

$$ v(t) = v_H - \frac{2 * deacceleration * t^2 * (3 * t_d - 2 * t)}{3 * t_d^2} $$

距離の式

$$ S_d(t) = v_H * t - \frac{deacceleration * t^3 * (2 * t_d - t)}{3 * t_d^2} $$

減速区間の時間

$$ {t_d} = \frac{3*(v_H - v_L)}{2 * deacceleration} $$

最後にグラフで確認します。
条件を $v_L=100, v_H=400, deacceleration=150$ として計算すると $$ t_d=3.0 $$ $$ S_d(t_d)=750 $$ となります。

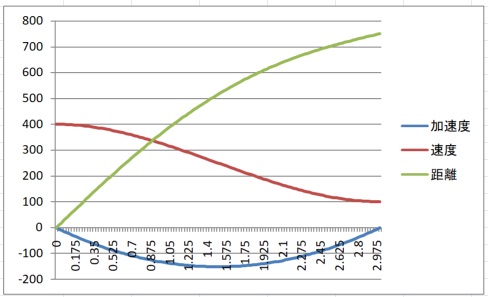
Destop View

距離優先の場合

移動距離を与えられた場合に最高速度を求めます。

$$ 加速区間の距離と減速区間の距離の合計が全体の移動距離S_{a+d}です。 $$ $$ S_a(t_a) + S_d(t_d) = S_{a+d} $$ $$ 上記の方程式を満たす最高速度v_Hを求める。 $$

$$ v_H = \sqrt{v_L^2 + \frac{4 * S_{a+d} * acceleration * deacceleration}{3 * (acceleration + deacceleration)}} $$

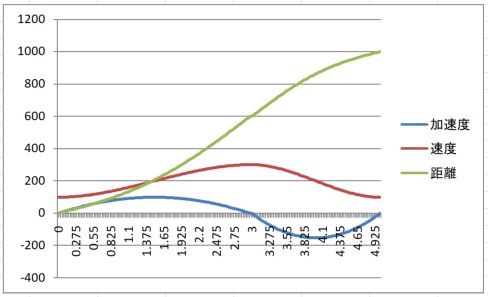
これをグラフで確認します。
条件を $S_{a+d}=1000, v_L=100, acceleration=100, deacceleration=150$ として計算すると $$ v_H=300.0 $$ $$ t_a=3.0 $$ $$ t_d=2.0 $$ $$ S_a(t_a)=600 $$ $$ S_d(t_d)=400 $$ となります。

Destop View

方向転換(片回転方式)

停止状態から外輪のみを回転させて方向転換を行う方式です。
内輪は停止状態のまま、外輪のみを駆動させる方程式を求めます。従って車輪間距離が旋回半径になります。

$$ Rc = Lwh $$

$$ S_{outer}(t) = \frac{Rc * 2 * \pi * spm * \theta(t)}{360} $$

加速区間

$$ 外輪の加速は直進での加速区間の方程式に従うので、 $$

$$ S_{outer_a}(t) = S_a(t) $$

$$ 角度について整理すると $$

$$ \theta_{a}(t) = \frac{80 * acceleration^2 * t^3 * (3 * v_H - acceleration * t)}{3 * Lwh * \pi * spm * v_H^2} $$

グラフで確認します。
条件を $v_L=0, v_H=200, acceleration=100$ として計算すると $$ t_a=3.0 $$ $$ \theta_{a}(t_a)=78.5 $$ となります。

Destop View

減速区間

加速区間と同様に求めます。

$$ S_{outer_d}(t) = S_d(t) $$

$$ \theta_{d}(t) = \frac{20 * t * (27 * v_H^3 - 12 * deacceleration^2 * t^2 * v_H + 4 * deacceleration^3 * t^3)}{3 * Lwh * \pi * spm * v_H^2} $$

グラフで確認します。
条件を $v_L=0, v_H=200, deacceleration=150$ として計算すると $$ t_d=2.0 $$ $$ \theta_{d}(t_d)=52.3 $$ となります。

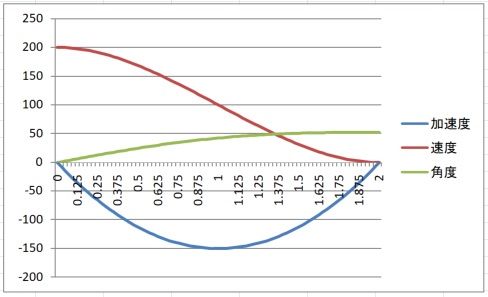
Destop View

角度優先の場合

与えられた角度から最高速度を求めます。

$$ \theta_{a}(t_a) + \theta_{d}(t_d) = \theta_{a+d} $$

$$ v_H = \sqrt{\frac{Lwh * \pi * acceleration * deacceleration * spm * \theta_{a+d}}{135 * (acceleration + deacceleration)}} $$

グラフで確認します。
条件を $\theta_{a+d}=45, v_L=0, acceleration=100, deacceleration=150$ として計算すると $$ v_H=117.2 $$ $$ t_a=1.7 $$ $$ t_d=1.2 $$ $$ \theta_a=27.0 $$ $$ \theta_d=18.0 $$ となります。

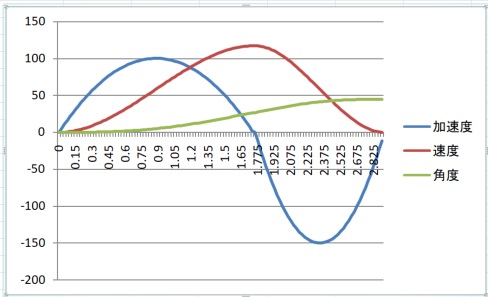
Destop View

方向転換(逆回転方式)

停止状態から両輪を逆回転させて方向転換を行う方式です。
旋回円の中心は両輪を結んだ直線の中点で、旋回円の直径は両輪間の長さです。
外輪・内輪の区別はありません。

$$ Rc = \frac{Lwh}{2} $$

$$ S_{left}(t) = S_{right}(t) = \frac{Rc * 2 * \pi * spm * \theta(t)}{360} $$

加速区間

$$ 両輪の加速は直進での加速区間の方程式に従うので、 $$

$$ S_{left_a}(t) = S_{right_a}(t) = S_a(t) $$

$$ \theta_a(t) = \frac{160 * acceleration^2 * t^3 * (3 * v_H - acceleration * t)}{3 * Lwh * \pi * spm * v_H^2} $$

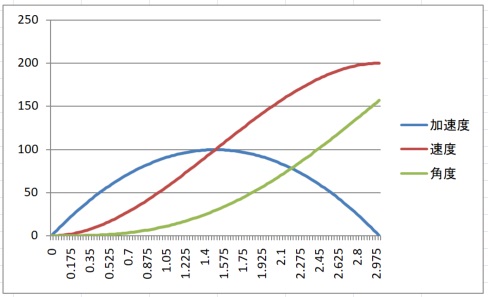
グラフで確認します。
条件を $v_L=0, v_H=200, acceleration=100$ として計算すると $$ t_a=3.0 $$ $$ \theta_a(t_a)=157.0 $$ となります。

Destop View

減速区間

加速区間と同様に求めます。

$$ S_{left_d}(t) = S_{right_d}(t) = S_d(t) $$

$$ \theta_d(t) = \frac{40 * t * (27 * v_H^3 - 12 * deacceleration^2 * t^2 * v_H + 4 * deacceleration^3 * t^3)}{3 * Lwh * \pi * spm * v_H^2} $$

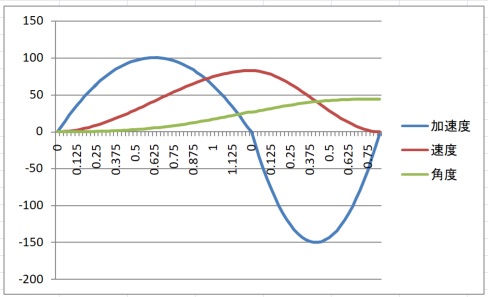
グラフで確認します。
条件を $v_L=0, v_H=200, deacceleration=150$ として計算すると $$ t_d=2.0 $$ $$ \theta_d(t_d)=104.7 $$ となります。

Destop View

角度優先の場合

与えられた角度から最高速度を求めます。

$$ \theta_a(t_a) + \theta_d(t_d) = \theta_{a+d} $$

$$ v_H = \sqrt{\frac{Lwh * \pi * acceleration * deacceleration * spm * \theta_{a+d}}{270 * (acceleration + deacceleration)}} $$

グラフで確認します。
条件を $\theta_{a+d}=45, v_L=0, acceleration=100, deacceleration=150$ として計算すると $$ v_H=82.9 $$ $$ t_a=1.2 $$ $$ t_d=0.8 $$ $$ \theta_a=27.0 $$ $$ \theta_d=18.0 $$ となります。

Destop View

進路変更

定速で走行中に外輪の速度を上げて進路変更を行います。外輪は加速・定速・減速を行います。内輪は一定速度を維持します。

$$ S_{inner}(t) = \frac{(Rc - \frac{Lwh}{2}) * 2 * \pi * spm * \theta(t)}{360} $$ $$ S_{outer}(t) = \frac{(Rc + \frac{Lwh}{2}) * 2 * \pi * spm * \theta(t)}{360} $$

加速区間

外輪は上記で求めた直進の加速区間と同じで、内輪は一定速度で時間を乗すれば走行距離となります。

$$ S_{outer}(t) - S_{inner}(t) = S_a(t) - (v_L * t) $$

$$ \theta_a(t) = \frac{80 * acceleration^2 * t^3 * (3 * v_H - 3 * v_L - acceleration * t)}{3 * Lwh * \pi * spm * (v_H - v_L)^2} $$

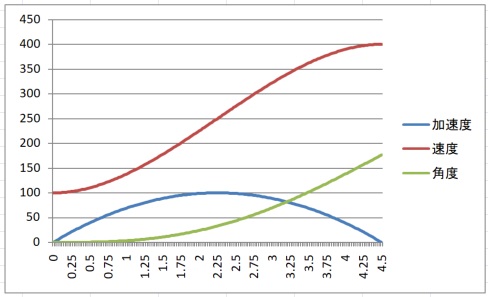
グラフで確認します。
条件を $v_L=100, v_H=400, acceleration=100$ として計算すると $$ t_a=4.5 $$ $$ \theta_a(t_a)=176.7 $$ となります。

Destop View

減速区間

減速区間も加速区間と同様の方法で方程式を立てます。

$$ S_{outer}(t) - S_{inner}(t) = S_d(t) - (v_L * t) $$

$$ \theta_d(t)= \frac{20 * t * (27 * (v_H^3 - v_L^3) - 81 * v_H * v_L * (v_H - v_L) - 12 * deacceleration^2 * t^2 * (v_H - v_L) + 4 * deacceleration^3 * t^3)}{3 * Lwh * \pi * spm * (v_H - v_L)^2} $$

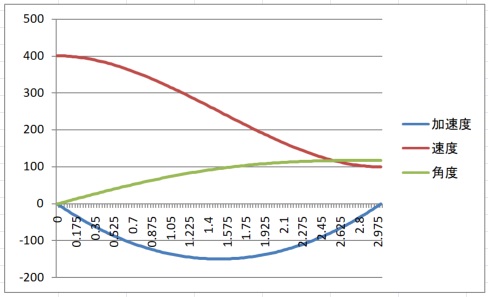
同様にグラフで確認します。
条件を $v_L=100, v_H=400, deacceleration=150$ として計算すると $$ t_d=3.0 $$ $$ \theta_a(t_a)=117.8 $$ となります。

Destop View

角度優先の場合

与えられた角度から最高速度を求めます。

$$ \theta_a(t_a) + \theta_d(t_d) = \theta_{a+d} $$

$$ v_H = v_L + \frac{\sqrt{15 * Lwh * \pi * acceleration * deacceleration * (acceleration + deacceleration) * spm * \theta_{a+d}}}{45 * (acceleration + deacceleration)} $$

グラフで確認します。
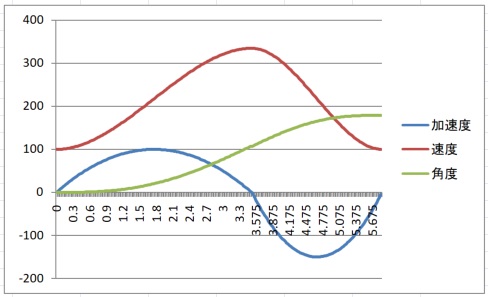
条件を $\theta_{a+d}=180, v_L=100, acceleration=100, deacceleration=150$ として計算すると $$ v_H=334.5 $$ $$ t_a=3.5 $$ $$ t_d=2.3 $$ $$ \theta_a=108.0 $$ $$ \theta_d=72.0 $$ となります。

Destop View

実装

自作の走行ロボットに実装しましたので、実際の動きを確かめてみます。滑らかな加速・減速が実現できました。

YouTube