Inverted Pendulum without Encoder
Overview
エンコーダーを使わない倒立振子を開発しました。
一般的に、倒立振子は振子部分の角度・角速度を測るジャイロセンサーと、
台車部分の速度・走行距離を測るエンコーダーの2つを用いますが、
エンコーダーは機械設計技術が必要だったり、使用できるモーターの種類が限定されたり、
高価であったり、と難易度が高いと思います。
そこで、エンコーダーを使わずにソフトウェアで代用する方法を考え、
シミュレーションと実装を行ったので、ここに紹介します。
Source Code
Source code may be found as the Python3 program in the GitHub repository.
github.com/HideoMiyauchi/InvertedPendulum
Usage
Very easy to get it working.
$ python InvertedPendulum.py
シミュレーション結果
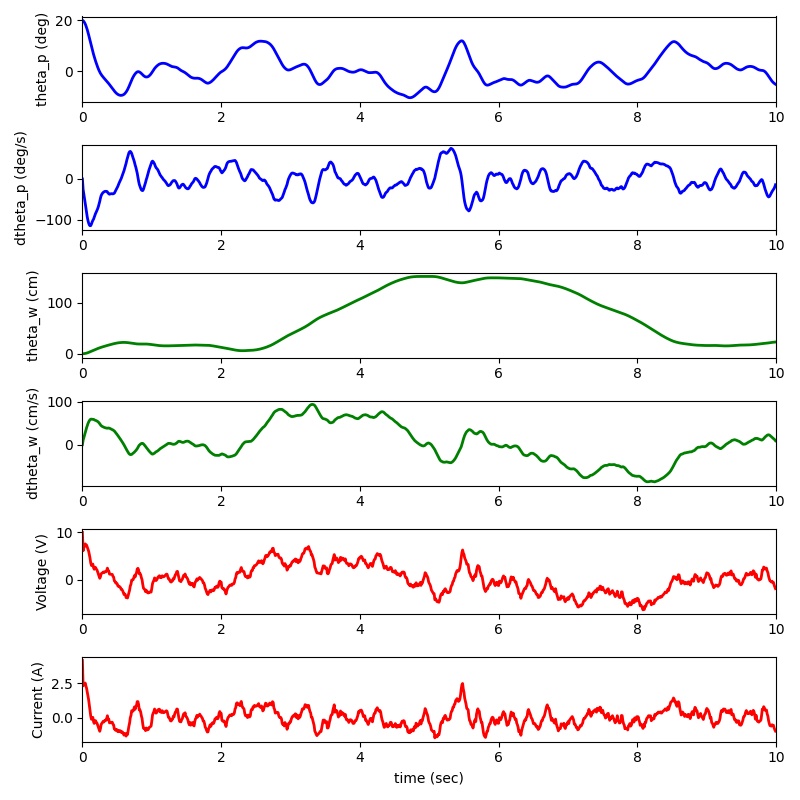
先に結果のシミュレーションを示し、内容については後述します。
振子の開始角20度。センサー値のドリフト有り。time=200〜400で右移動、time=600〜800で左移動を
行うシミュレーションです。解析がしやすいようにセンサーにノイズを含めない場合と、
実際のセンサーのようにノイズを含める場合の2つのシミュレーションを示します。ノイズは正規分布に従っています。
グラフは上から、振子角度、振子角速度、移動距離、移動速度、モーター印加電圧、モーター電流です。
ご覧のようにエンコーダが無くても、time=0〜200で開始角20度から0度に収束し、time=200〜で左右移動を行っても倒立は実現できています。
移動距離にオフセットが残ってる部分や移動速度がゼロになっていない部分はエンコーダーを完全に代用できていないことが原因だと考えられます。
センサーにノイズを含めない場合
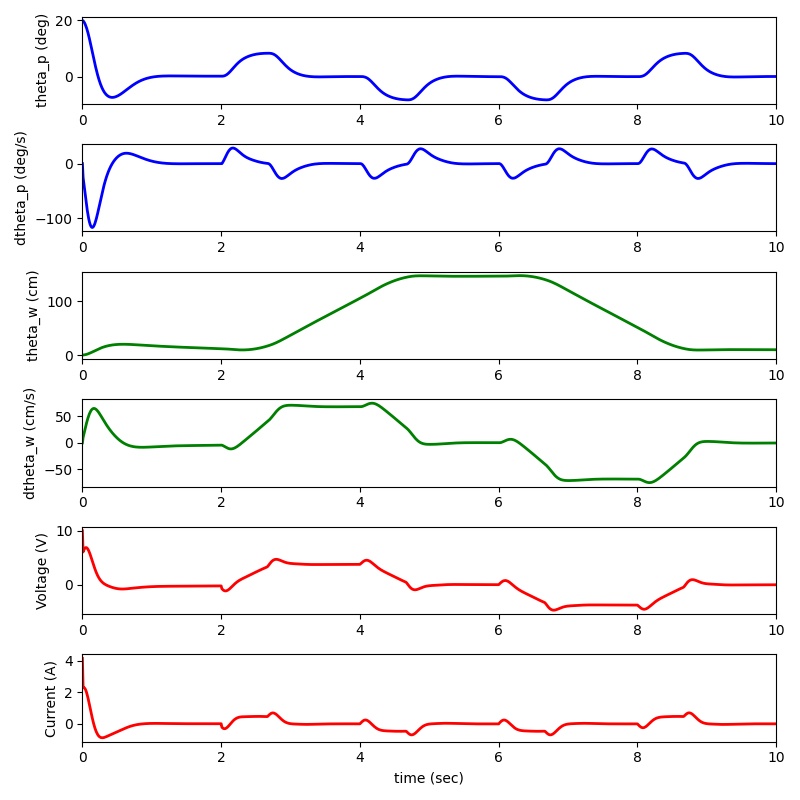
センサーにノイズを含める場合
エンコーダーを使わない方法とは
モーター印加電圧は車輪の速度と比例する、と考えます。 実際はモーター出力が線形では無いため、厳密には比例しませんが、 誤差部分は移動距離、移動速度に影響を及ぼし、ふらつきの原因となるはずです。 ただし、モーターへの印加から実際に動き出すまでにはタイムラグがあるので、 モーター印加電圧を遅延フィルターに通し、さらにレベルを合わせることで車輪の速度とします。
シミュレーションの内容
シミュレーションに使用した倒立振子モデルは、トラ技1で紹介されていたものに 手を加えています。最適フィードバックゲインなどはそのまま用いています。 手を加えた部分について説明していきます。
倒立振子の微分方程式の数値解をルンゲ=クッタ法で求めます。xは状態変数、Vinはモーター印加電圧です。
#calculate the next state
x = rungeKuttaSolver(i, x, T, Vin)
角速度の状態変数にドリフトとノイズを加えたものをジャイロセンサーと考えます。 そして、そのジャイロセンサーの出力をローパスフィルターへ通します。
#simulate gyro sensor
rawGyro = np.random.normal(x[1][0] + driftGyro, scale=scaleGyro)
k = 0.3
nowGyroOmega = (1 - k) * beforeGyroOmega + k * rawGyro
角度の状態変数にドリフトとノイズを加えたものを加速度センサーと考えます。 そして、その加速度センサーの出力をローパスフィルターへ通します。
#simulate accelerometer
rawAccel = np.random.normal(x[0][0] + driftAccel, scale=scaleAccel)
k = 0.3
nowAccelTheta = (1 - k) * beforeAccelTheta + k * rawAccel
次に、相補フィルターを使って振子の角度を計算します。
#calculate the angle using complementary filter
k = 0.06
nowTheta = (1 - k) * (beforeTheta + nowGyroOmega * T) + k * nowAccelTheta
これがエンコーダーをソフトウェアで代用した部分です。
モーター印加電圧を遅延フィルターへ通し、レベルを合わせることで移動速度を求めています。
#speed is proportional to the delayed motor voltage
k = 0.05
nowDelayedVin = (1 - k) * beforeDelayedVin + k * beforeVin
nowSpeed = nowDelayedVin * 8 # level matching
上で求めた移動速度を積分して移動距離を求めます。
#calculate the distance by integrating the velocity
nowDistance = beforeDistance + (nowSpeed + beforeSpeed) * T / 2
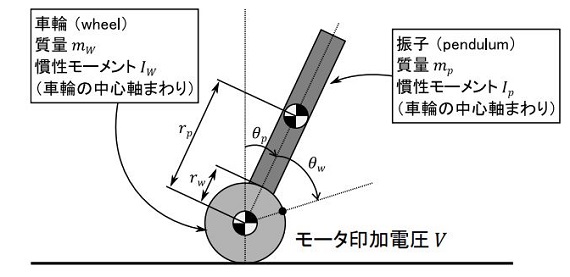
倒立振子の力学モデル
トラ技1で紹介されていた倒立振子モデルを載せておきます。 確率・統計・数学の予備知識も記載されている良い本だと思います。 なお、ソースコードはCQ出版社のHPからダウンロードできます。
倒立振子の力学モデル
$$ \lbrace ( m_w + m_p ) r_w^2 + 2 m_p r_w r_p \cos(\theta_p) + m_p r_p^2 + I_p + I_w \rbrace \ddot \theta_p $$
$$ + \lbrace ( m_w + m_p ) r_w^2 + m_p r_w r_p \cos(\theta_p) + I_w \rbrace \ddot \theta_w $$
$$ - m_p r_w r_p \dot \theta_p^2 \sin(\theta_p) - m_p g r_p \sin(\theta_p) = 0 $$
$$ \lbrace ( m_w + m_p ) r_w^2 + m_p r_w r_p \cos(\theta_p) + I_w \rbrace \ddot \theta_p $$
$$ + \lbrace ( m_w + m_p ) r_w^2 + I_w + n^2 I_m \rbrace \ddot \theta_w $$
$$ - m_p r_w r_p \dot \theta_p^2 \sin(\theta_p) + n^2 \frac{k_t k_b}{R} \dot \theta_w $$
$$ = n \frac{k_t}{R} ( V - \frac{R}{k_t} \tau_m’ ) $$
線形近似して得られた「状態方程式」
$$ \left\lceil\matrix{ \dot \theta_p \cr \ddot \theta_p \cr \dot \theta_w \cr \ddot \theta_w }\right\rceil =\left\lceil\matrix{ 0, & 1, & 0, & 0\cr \frac{a_{22} m_p g r_p}{\Delta}, & 0, & 0, & \frac{a_{12} n^2 k_t k_b / R}{\Delta}\cr 0, & 0, & 0, & 1\cr \frac{-a_{21} m_p g r_p}{\Delta}, & 0, & 0, & \frac{-a_{11} n^2 k_t k_b / R}{\Delta} }\right\rceil \left\lceil\matrix{ \theta_p \cr \dot \theta_p \cr \theta_w \cr \dot \theta_w }\right\rceil $$
$$ +\left\lceil\matrix{ 0 \cr \frac{-a_{12} n k_t / R}{\Delta} \cr 0 \cr \frac{a_{11} n k_t / R}{\Delta} }\right\rceil ( V - V_{offset} ) $$
$$ a_{11} = (m_w + m_p) r_w^2 + 2 m_p r_w r_p + m_p r_p^2 + I_p + I_w $$ $$ a_{12} = (m_w + m_p) r_w^2 + m_p r_w r_p + I_w $$ $$ a_{21} = (m_w + m_p) r_w^2 + m_p r_w r_p + I_w $$ $$ a_{22} = (m_w + m_p) r_w^2 + I_w + n^2 I_m $$ $$ \Delta = a_{11} a_{22} - a_{12} a_{21} $$
| 定数名 | 説明 | 値 |
|---|---|---|
| \(m_w\) | タイヤの1個分の質量 (kg) | 0.026 |
| \(m_p\) | 倒立振子本体の質量 ÷ 2 (kg) | 0.208 |
| \(r_w\) | タイヤの半径 (m) | 0.028 |
| \(r_p\) | 車軸から車体の重心までの距離 (m) | 0.08735 |
| \(I_w\) | 車軸まわりの,タイヤ1個分の慣性モーメント (kg・m2) | 1.0192×10-5 |
| \(I_p\) | 車軸まわりの,車体の慣性モーメント ÷ 2 (kg・m2) | 0.001587 |
| \(I_m\) | モータ軸まわりの,モータ回転子の慣性モーメント (kg・m2) | 2.8125×10-7 |
| \(n\) | ギアボックスのギア比 | 64.8 |
| \(k_t\) | モータのトルク定数 (N・m/A) | 0.0018 |
| \(k_b\) | モータの逆起電力定数 (V・sec/rad) | 0.0024 |
| \(R\) | モータおよびモータ・ドライバの等価直列電気抵抗 (Ω) | 2.4 |
| \(V_{offset}\) | 摩擦トルクの影響による実効的なモータ電圧のオフセット(V) ※Vinが正ならプラス,Vinが負ならマイナス |
±0.17 |
| \(g\) | 重力加速度 (m/s2) | 9.8 |
実装
手のひらサイズの倒立振子を作りました。単四乾電池3本で動きます。
当然ですが、諸元についてはシミュレータと異なります。
他にも
- 加速度センサーは使っていません。当然、相補フィルターもありません。
- 移動は速度では無く、距離のパラメーターを変化させて実現しています。
の点がシミュレータと異なります。
では、実際の動きをご覧下さい。
最後に
エンコーダー無しの倒立振子を開発できました。
静止状態は安定しており、
他のエンコーダー有りと比べても遜色ないものになりました。
移動させた場合の距離はアバウトになってしまっていますが、
これは致し方ないでしょう。
Reference

 CQ出版社 2019年7月号
CQ出版社 2019年7月号